Question

LCM of polynomials 5y^2 - 80 and y + 4

Answer 1

facctore each

5y^2=5*y*y
80=5*2*2*2*2
lcm of those are
5
5(y^2-16)
we can factor this difference of 2 perfect squares
5(y-4)(y+4)


y+4 is the other one


so the lcm is 5y^2-80

Answer 2

The Least Common Multiple of polynomials is

`5(y+4)(y-4)`

Explanation:

Given : Polynomials
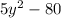`5y^2-80` and
`y+4`

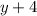
To find : LCM of the given polynomials

Solution :

First we find the factors of the polynomial
`5y^2-80`

`5y^2-80=5(y^2-16)`

`5y^2-80=5(y^2-4^2)`

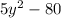
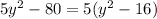
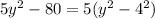
Apply
`a^2-b^2=(a+b)(a-b)`

`5y^2-80=5(y+4)(y-4)`

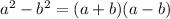
The LCM of some numbers is the smallest number that the numbers are factors of.

The LCM of 5 is result of multiplying all prime factors, the greatest number of times they occur in either number.

So, LCM of 5 is 5

The LCM of (y+4)(y-4),(y+4) is the result of multiplying all factors, the greatest number of times they occur in either term.

So, LCM of (y+4)(y-4),(y+4) is (y+4)(y-4)

Therefore, The Least Common Multiple of polynomials is
`5(y+4)(y-4)`