Question

Calculus(Integration): How would I go about solving this problem? Would I have to make them equal to each other to find the limits of integration and then subtract the limits from each equation and then each other? Thanks in advance!

Answer 1

Judging by the 72 in the bottom right corner of your image, I'm going to assume the answer to my question above is "yes".

First, find the intersections of the parabolas.


`x^2-4x=16-x^2`

`\implies 2x^2-4x-16=0`

`\implies x=-2,x=4`

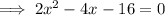
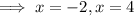
Now the area is given by the integral


`\displaystyle\int_(-2)^4|(x^2-4x)-(16-x^2)|\,\mathrm dx`

But over the interval
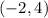
`(-2,4)` (and just by looking at the graph, you know this), you have
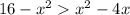
`16-x^2>x^2-4x`, which means


`|(x^2-4x)-(16-x^2)|=(16-x^2)-(x^2-4x)`

which follows from the definition of absolute value. Then the integral reduces to


`\displaystyle\int_(-2)^4(16+4x-2x^2)\,\mathrm dx`

Integrating term-by-term yields


`\left(16x+2x^2-\frac23x^3\right)\bigg|_(x=-2)^(x=4)=72`

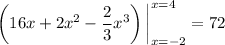
as required.