Answer:
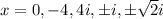
Explanation:
The given equation is
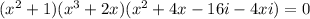
According to zero product of property, if ab=0, then either a=0 or b=0.
Using zero product property we get
Case 1:
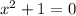

Taking square root on both sides.
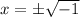

![[\because √(-1)=i]](https://img.qammunity.org/2018/formulas/mathematics/high-school/d39fprobob57yygbyvg1r3bz2xx1320z25.png)
Case 2:
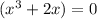
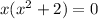
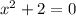 and
and


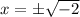

Case 3:
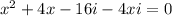
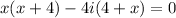
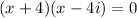
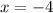
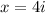
Therefore, the roots of given equation are
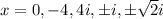 .
.