Answer:
A). 31.43°
B). 225 feet
Explanation:
A) From the given equation for horizontal distance h of a projectile is given by
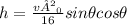
If initial velocity v0 = 60 ft/sec and horizontal distance = 100 feet
Then the equation will be
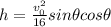

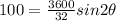
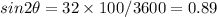
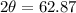
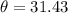
B). If v0 = 60 feet per second
Then we have to calculate the maximum horizontal distance and angle.
Since we know to cover the maximum distance in a projectile motion an object should be thrown at 45°.
Therefore the equation formed will be
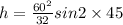
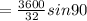
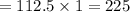
h = 112.5 feet