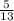Answer:
sin A =
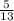
Explanation:
As per the statement:
∠A is an acute angle in a right triangle.
Given that:
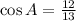
We have to find Sin A:
Using the formula:

Substitute the given values we have;
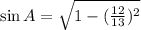
⇒
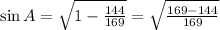
⇒

Therefore, the value of sin A as a fraction in simplest form is,