Answer:
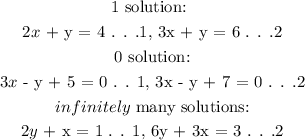
Step-by-step explanation:
We need to give an example of 2 systems of linear equation where we have 0 solution, 1 solution and infinitely many solution. Then we will provide an explanation to determine each of them without graphing.
Example for 1 solution:
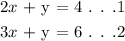
To ascertain the two linear equations give one solution, we will have a value for x
Subtract equation (1) from (2):
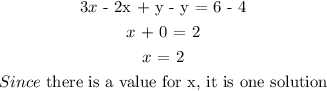
Example for 0 solution:
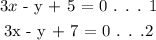
To determine 0 solution system of linear equations, when we solve for the variable the left hand side will not be equal to the right hand
solving the above linear equation:

Example of infintely many solutions:
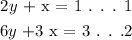
To determine that the solution is infinitely many solutions, the left hand side will be equal to right hand side.
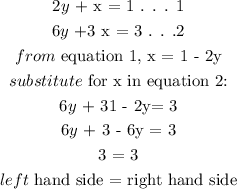
Behaviour of the solution of the system of equations when graphed:
For a system of 2 linear equations with 1 solution:
The lines will intersect at a point. The point of intersection is 1 and it will be the solution of the system of equations
For a system of 2 linear equations with 0 solution:
The lines from both equations will be parallel to each other. Indicating the lines do not intersect. Hence, there is no solution
For a system of 2 linear equations with infinitely many solutions:
Both equation will give same line when graphed. So, the solution will be infinitely many