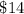Question

1) Cody's school is selling tickets to a spring musical. On the first day of ticket sales the school sold 5senior citizen tickets and 3 student tickets for a total of $92. The school took in $72 on the secondday by selling 3 senior citizen tickets and 3 student tickets. Find the price of a senior citizen ticketand the price of a student ticket.

Answer 1

Given that:

- On the first day the school sold 5 senior citizen tickets and 3 student tickets for a total of $92.

- On the second day the school took in $72 by selling 3 senior citizen tickets and 3 student tickets.

Let be "x" the price (in dollars) of a senior citizen and "y" the price (in dollars) of a student ticket.

Using the data provided in the exercise, you can set up this System of Equations:

`\begin{cases}5x+3y={92} \\ 3x+3y={72}\end{cases}`

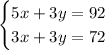
You can solve it using the Elimination Method:

1. Multiply the first equation by -1.

2. Add the equations.

Then:

`\begin{gathered} \begin{cases}-5x-3y={-92} \\ 3x+3y={72}\end{cases} \\ --------- \\ -2x+0=-20 \\ -2x=-20 \end{gathered}`

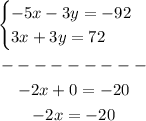
3. Solve for "x":

`\begin{gathered} x=(-20)/(-2) \\ \\ x=10 \end{gathered}`

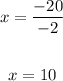
4. Substitute the value of "x" into one of the original equations and solve for "y":

`\begin{gathered} 3(10)+3y=72 \\ 3y=72-30 \\ \\ y=(42)/(3) \\ \\ y=14 \end{gathered}`

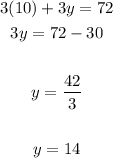
Hence, the answer is:

- Price of a senior citizen ticket:

`\text{ \$}10`

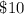
- Price of a student ticket:

`\text{ \$}14`