Answer: 1, 235, 520 different arrangements
Explanation: Since we want to arrange them, we care about the order in which they come in.
Let's firstly think about it in a diagrammatic way before diving into the permutations side of things.
We have 13 swimmers, let's name them from 1 to 13. Now, we want to arrange six of them in a line (hypothetically).
Thus, we can arrange the first six people:
1 2 3 4 5 6
1 2 3 4 6 5
1 2 3 6 5 4
1 2 3 6 4 5
...
In fact, we have 6! ways in arranging six objects into six places, which is 720 different ways.
Now, let's think about it in a bigger spectrum. If we have 13 people and we want to arrange them in 13 blocks, we would have 13! ways in arranging them:
Different permutations:
Ways in arranging 13 people into 13 different lanes is given by:
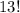
Now, we want to restrict that into 6 blocks, so we can only have 6 people in it
So, we would have (13 - 6)! ways in arranging them into 6 blocks.
So, our final number of arrangements is:
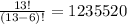
ways.
This is also the formula for the Permutation function represented by:
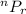
, where n is the number of objects (13) and r is the number of positions (6).