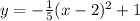Question

Find the vertex of the function y = (-1/5)x2 + (4/5)x + 1/5.

Answer 1

(2, 1)

Step-by-step explanation:

Given:

`-(1)/(5)x^2+(4)/(5)x+(1)/(5.)`

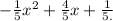
To find:

The vertex of the function

Step-by-step solution:

To be able to determine the vertex of the given function, we have to rewrite the function in the below vertex form;

`y=a(x-h)^2+k`

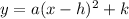
where (h, k ) is the vertex of the function.

Recall that a quadratic equation in general form is given as;

`y=ax^2+bx+c`

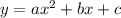
If we compare the above equation with the given equation, we see that a = -1/5, b = 4/5, and c = 1/5

We'll find the value of h using the below formula;

`\begin{gathered} h=-(b)/(2a) \\ h=-((4)/(5))/(2(-(1)/(5))) \\ h=(-(4)/(5))/(-(2)/(5)) \\ h=-(4)/(5)*(-(5)/(2)) \\ h=(4)/(2) \\ h=2 \end{gathered}`

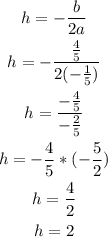
We can now determine the value of k as seen below;

`\begin{gathered} k=f(h) \\ \\ k=-(1)/(5)(2)^2+(4)/(5)(2)+(1)/(5) \\ \\ k=-(4)/(5)+(8)/(5)+(1)/(5) \\ \\ k=(-4+8+1)/(5) \\ \\ k=(5)/(5) \\ \\ k=1 \end{gathered}`

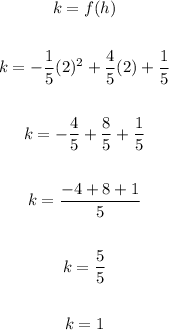
Since h = 2 and k = 1, then the vertex of the function is (2, 1) and we can write the function in vertex form as;

`y=-(1)/(5)(x-2)^2+1`