Answer:
A:
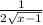
B:
![\frac{1}{4\sqrt[4]{x^(3) } }](https://img.qammunity.org/2022/formulas/mathematics/high-school/zklofudja0tibreuyamjlmdd1j5s0u0o8e.png)
c: 2x
Explanation:
To find the derivative of x raised to the nth power we use the following template
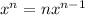
Something else to keep in mind is that
![\sqrt[n]{x^(y)}=x^(y/n)](https://img.qammunity.org/2022/formulas/mathematics/high-school/dbtmo3igxjkf7p7di1hiim12qm9e3hdyfr.png)
So knowing this we can rewrite a as follows

so we can use the template above and get
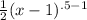
So that simplifies to
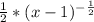
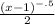
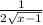
B: Same kind of deal here
![\sqrt[4]{x}=x^{(1)/(4) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/a0zmnwpqfzkmxf5bpzkvlz0287it1imqgo.png)
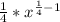
![\frac{x^{-(3)/(4)}}{4} =\frac{1}{4\sqrt[4]{x^(3) } }](https://img.qammunity.org/2022/formulas/mathematics/high-school/qb0zbtarbbm7i8w36kcnt9qt1noqu1c9he.png)
C: this one is by far the easiest because the derivative of a constant is 0 so we can just apply the same template from before and get
2x