Question

An equation for the depreciation of a car is given by y = A(1 – r)t , where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years. The value of a car is half what it originally cost. The rate of depreciation is 10%. Approximately how old is the car?

Answer 1

.5A = A(1 - 0.1)^t
.5 = (0.9)^t
log_(0.9)(0.5) = t
t = ln(.5)/ln (.9)

The car is approximately 7 years old

Answer 2

`t=6.578813479\approx 7\hspace{3}years`

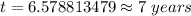
Explanation:

Basically we need to find the value of t, according to the data suply by the problem. The problem gives this equation:

`y=A(1-r)^t`

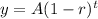
In this case, the problem tell us:

`y=(A)/(2) \\r=10\%=0.1`

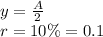
Replacing the data in the equation:

`(A)/(2) =A(1-0.1)^t`

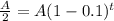
Divide both sides by A:

`(A)/(2A)=(A)/(A)(1-0.1)^t\\(1)/(2) =(0.9)^t`

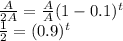
Now, simply take the logarithm base 0.9 of both sides:

`log_0_._9((1)/(2))=log_0_._9(0.9)^t\\ \\6.578813479=t`

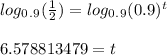
Therefore:

`t=6.578813479\approx 7\hspace{3}years`

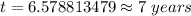
The car is approximately 7 years old