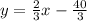Given the equation of a line, we can use the slope to find the slope of a perpendicular line. If we call m the slope, then the slope of a perpendicular line is:

Now, we are given the equation of the line:
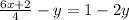
To find the slope, we need to rewrite this in slope-intercept form. To do this, we need to solve for y:
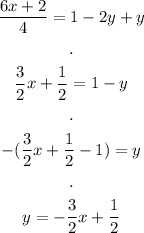
Then, the slope of this line is -3/2. The slope of a line perpendicular to it is the inverse of the reciprocal:
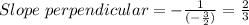
Now, we know that the slope of the line perpendicular is 2/3, and it must pass through the point (5, -10). We can use the slope- point fomr of a line.
The point-slope form of a line, given slope m and a point P is:
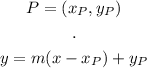
IN the perpendicular line, m = 2/3 and P = (5, -10):

And solve:
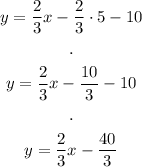
The answer is: