Question

After turning a map into a directed graph then into a matrix, I have been asked to square the matrix in class. I ran into this question that asked me to explain what the squared matrix represents. Does anyone know?

-
Alice and Becky live on Parkway East, at the intersections of Owens Bridge and Bay Bridge, respectively. Carl and David live on Parkway West, at the intersections of Bay Bridge and Owens Bridge, respectively. Parkway East is a one-way street running east. Parkway West is one way running west. Both bridges are two way. Calculate What does the new matrix model represent? Explain.

Answer 1

I'm assuming that by "turning the graph into a matrix" you're referring to the adjacency matrix associated with a given directed graph, which encodes a connection between two vertices
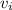
`v_i` and
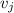
`v_j` by the number
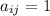
`a_(ij)=1` if there's an edge beginning at
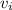
`v_i` and terminating at
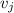
`v_j` and 0 otherwise. Here
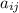
`a_(ij)` is the entry of the adjacency matrix
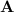
`\mathbf A` in the
`i`th row and
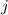
`j`th column.


`a_(ij)=\begin{cases}1&\text{if }v_i\to v_j\\0&\text{otherwise}\end{cases}`

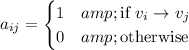
Let's consider a simple example of a graph
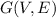
`G(V,E)` on three vertices
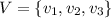
`V=\{v_1,v_2,v_3\}`, where the edge set is
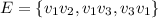
`E=\{v_1v_2,v_1v_3,v_3v_1\}`. (image below)

The corresponding adjacency matrix is


`\mathbf A=\begin{bmatrix}0&1&1\\0&0&0\\1&1&0\end{bmatrix}`

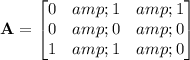
and squaring this gives the matrix


`\mathbf B=\mathbf A^2=\begin{bmatrix}1&1&0\\0&0&0\\0&1&1\end{bmatrix}`

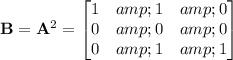
Let's think about what the entry
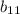
`b_(11)` is saying. We obtained it by computing the vector product,


`b_(11)=a_(1j)\cdot a_(i1)=\begin{bmatrix}0&1&1\end{bmatrix}\begin{bmatrix}0\\0\\1\end{bmatrix}=0\cdot0+1\cdot0+1\cdot1=1`

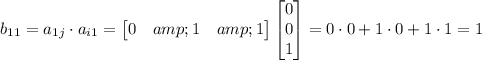
We can interpret each term as counting the number of two-step paths we can take starting from
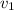
`v_1` and ending up back on
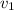
`v_1`. We'll require that staying in place is not an option, that a path from one vertex to itself must involve leaving the first vertex.

The first term is then 0, since there is no path from
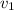
`v_1` to itself:
`a_(1,1)\cdot a_(1,1)=0`

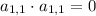
The second term is also 0, since we can take a step from
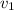
`v_1` over to
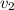
`v_2`, but we can't go back:
`a_(1,2)\cdot a_(2,1)=0`

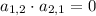
The third term is 1, because we can take a step from
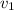
`v_1` to
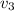
`v_3`, and we can then undo that step by going backwards from
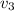
`v_3` to
`v_1`:
`a_(1,3)\cdot a_(3,1)=1`

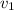
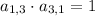
And so on. We can make the claim that
`b_(ij)` (the
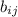
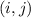
`(i,j)`th element of
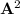
`\mathbf A^2`) will give you the number of 2-edge paths from
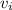
`v_i` to
`v_j`.

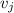
And more generally,
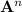
`\mathbf A^n` will give the number of paths consisting of
`n` steps.