Answer:
The height of rocket is 102.7 meter.
Explanation:
Given : Brynn and Denise launch their rockets at the same time.
The height of Brynn’s rocket, in meters, is given by the function
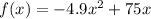 , where x is the number of seconds after the launch.
, where x is the number of seconds after the launch.
The height of Denise’s rocket, in meters, is given by the function
 , where x is the number of seconds after the launch.
, where x is the number of seconds after the launch.
There is a moment when the rockets are at the same height.
To find : The height
Solution :
When the rockets have same height
So,
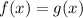

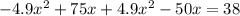
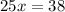

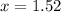
Now, we put x value in any of the function to find height.
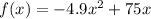 , x=1.52
, x=1.52
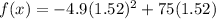

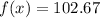
Nearest tenth = 102.7
Therefore, The height of rocket is 102.7 meter.