Answer:
Maximum height is 144 feet.
Explanation:
A quadratic equation y =
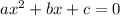 gives maximum value when x =
gives maximum value when x =
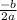
after finding the value of x we plug value of x in original equation in order to find the maximum value (minimum value in case of a >0)
on comparing given quadratic equation which is variable 't' ,we get a =-16 and b =64
t =
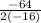
plugging this value of t =2 in original equation in order to get maximum value of h
so h =
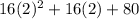
which gives h =144 feet