Question

More series issues!

For #10, I have found that when p <= 0, the series converges. Fact check on that?

Answer 1

It can't be that
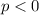
`p<0` makes the series converge, because this would introduce a zero in the denominator when
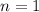
`n=1`. For a similar reason,
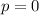
`p=0` would involve an indeterminate term of
`0^0`.

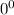
That leaves checking what happens when
`p>0`. First, consider the function


`f(x)=\frac{(\ln x)^p}x`

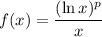
and its derivative


`f'(x)=(p(\ln x)^(p-1)-(\ln x)^p)/(x^2)=((\ln x)^(p-1))/(x^2)(p-\ln x)`


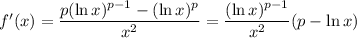
`f(x)` has critical points at
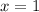
`x=1` and
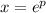
`x=e^p`. (These never coincide because we're assuming
`p>0`, so it's always the case that
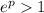
`e^p>1`.) Between these two points, say at
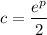
`c=\frac{e^p}2`, you have
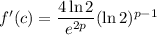
`f'(c)=(4\ln2)/(e^(2p))(\ln2)^(p-1)`, which is positive regardless of the value of
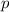
`p`. This means
`f(x)` is increasing on the interval
`(1,e^p)`.

Meanwhile, if
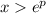
`x>e^p` - and let's take
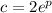
`c=2e^p` as an example - we have
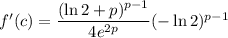
`f'(c)=((\ln2+p)^(p-1))/(4e^(2p))(-\ln2)^(p-1)`, which is negative for all
`p>0`. This means
`f(x)` is decreasing for all
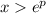
`x>e^p`, which shows that
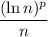
`\frac{(\ln n)^p}n` is a decreasing sequence for all
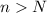
`n>N`, where
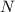
`N` is any sufficiently large number that depends on
`p`.

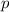
Now, it's also the case that for
`p>0` (and in fact all
`p\in\mathbb R`),


`\displaystyle\lim_(n\to\infty)\frac{(\ln n)^p}n=0`

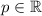
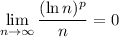
So you have a series of a sequence that in absolute value is decreasing and converging to 0. The alternating series then says that the series must converge for all
`p>0`.

For the second question, recall that


`h_n=\displaystyle\sum_(k=1)^n\frac1k=1+\frac12+\cdots+\frac1{n-1}+\frac1n`

`s_n=\displaystyle\sum_(k=1)^n\frac{(-1)^(k-1)}k=1-\frac12+\cdots-\frac1{n-1}+\frac1n`

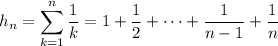
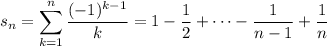
(note that the above is true for even
`n` only - it wouldn't be too difficult to change things around if
`n` is odd)

It follows that


`h_(2n)=\displaystyle\sum_(k=1)^(2n)\frac{(-1)^(k-1)}k=1+\frac12+\cdots+\frac1{2n-1}+\frac1{2n}`

`s_(2n)=\displaystyle\sum_(k=1)^(2n)\frac{(-1)^(k-1)}k=1-\frac12+\cdots+\frac1{2n-1}-\frac1{2n}`

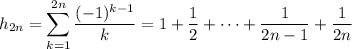
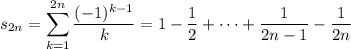
Subtracting
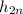
`h_(2n)` from
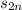
`s_(2n)`, you have


`\displaystyle s_(2n)-h_(2n)=(1-1)+\left(-\frac12-\frac12\right)+\left(\frac13-\frac13\right)+\left(-\frac14-\frac14\right)+\cdots+\left(\frac1{2n-1}-\frac1{2n-1}\right)+\left(-\frac1{2n}-\frac1{2n}\right)`

`s_(2n)-h_(2n)=-1-\frac12-\cdots-\frac2{2n}`

`s_(2n)-h_(2n)=-\left(1+\frac12+\cdots+\frac1n\right)`

`s_(2n)-h_(2n)=-h_n`

`\implies s_(2n)=h_(2n)-h_n`

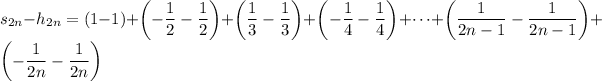
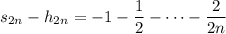
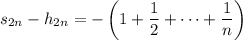
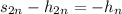
as required. Notice that assuming
`n` is odd doesn't change the result; the last term in
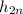
`h_(2n)` ends up canceling with the corresponding term in
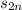
`s_(2n)` regardless of the parity of
`n`.