Question

Suppose that grade point averages of undergraduate students at one university have a bell-shaped distribution with a mean of 2.54 and a standard deviation of 0.42. Using the empirical rule, what percentage of the students have grade point averages that are between 1.7 and 3.38?I believe the answer to be 0.15% but I'm not too sure

Answer 1

The empirical rule of the bell-shaped distribution is:

• 68% of the data will be inside the interval of 1 standard deviation from the mean

,

• 95% of the data is data will be inside the interval of 2 standard deviations from the mean

,

• 99.7% of the data will be inside the interval of 3 standard deviations from the mean.

The representations for the mean and standard deviation are:

`\begin{gathered} \mu\longrightarrow\text{ mean} \\ \sigma\longrightarrow s\tan dard\text{ deviation} \end{gathered}`

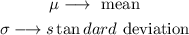
The following diagram represents the empirical rule:

In this case:

`\begin{gathered} \mu=2.54 \\ \sigma=0.42 \end{gathered}`

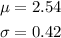
Calculating the values for the marks on the graph:

`\begin{gathered} \mu+\sigma=2.54+0.42=2.96 \\ \mu+2\sigma=2.54+2(0.42)=2.54+0.84=3.38 \\ \mu-\sigma=2.54-0.42=2.12 \\ \mu-2\sigma=2.54-2(0.42)=2.54-0.84=1.7 \end{gathered}`

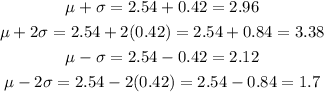
Substituting these values into our diagram:

As you can see, between 1.7 and 3.38 which is the interval between a distance of 2 standard deviations from the mean, we have 95% of the data, in this case, 95% of the students will have grade points averages that are between 1.7 and 3.38.

Answer: 95%