Question

What is the inverse of f(x)=2log3x

Answer 1

`y = 2log_3 x`

`x = 2log_3 y`

`log_3 y = (x)/(2)`

`3^(log_3 y) = 3^{(x)/(2)}`


`y = 3^{(x)/(2)}`
Hence,
`f^(-1)(x) = 3^{(x)/(2)}`

Answer 2

Assuming log is the natural logarithm:

`f^(-1)(x)=(e^(x/2))/(3)`

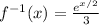
Assuming log is the base 10 logarithm:

`f^(-1)(x)=(10^(x/2))/(3)`

Explanation:

Assuming log is the natural logarithm:

First step: Replace f(x) with y that is
`f(x)=y`

`y=2log(3x)`

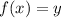
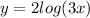
Second step: Solve for x:

`y=2log(3x)\\\\(y)/(2) =log(3x)`

`e^{(y)/(2) }=e^(log(3x))\\\\e^{(y)/(2) }=3x\\\\\frac{e^{(y)/(2) }}{3} =x`

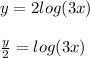
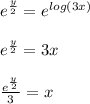
Third step: Replace every x with a y and replace every y with an x:

`\frac{e^{(x)/(2) }}{3} =y`

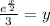
Final step: Replace y with
`f^(-1)(x)`:

`f^(-1)(x)=(e^(x/2))/(3)`

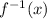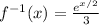
Assuming log is the base 10 logarithm:

It is the same procedure as before, the only thing that change, is when we are solving for x:

First step: Replace f(x) with y that is
`f(x)=y`

`y=2log(3x)`

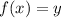
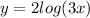
Second step: Solve for x:

`y=2log(3x)\\\\(y)/(2) =log(3x)`

`10^{(y)/(2) }=10^(log(3x))\\\\10^{(y)/(2) }=3x\\\\\frac{10^{(y)/(2) }}{3} =x`

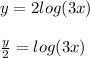
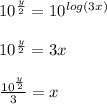
Third step: Replace every x with a y and replace every y with an x:

`\frac{10^{(x)/(2) }}{3} =y`

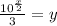
Final step: Replace y with
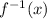`f^(-1)(x)` :

`f^(-1)(x)=(10^(x/2))/(3)`