Answer:
x = 1.1 and x = -2.43
Explanation:
We have the quadratic equation,
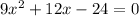 i.e.
i.e.
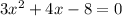
Now, we know that,
'The quadratic formula to find the solution of
 is given by
is given by
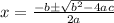 .
.
On comparing, we get from the given equation,
a= 3, b= 4 and c= -8
Substituting these values in the given quadratic formula, we get,
 .
.
i.e.
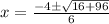 .
.
i.e.
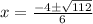
i.e.
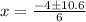
i.e.
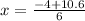 and
and
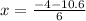
i.e.
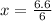 and
and
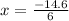
i.e. x = 1.1 and x = -2.43
Thus, the solution of the quadratic equation
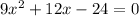 using the quadratic formula is x = 1.1 and x = -2.43.
using the quadratic formula is x = 1.1 and x = -2.43.