Question

A clerk was asked to change a $10 bill. She returned 9 more dimes than nickels and twenty-one more quarters than dimes. How many coins of each did she return? WRITER

Answer 1

so.. let's say, the amount of dimes is "d" and nickels is "n" and quarters is "q"

"She returned 9 more dimes than nickels", so.. whatever "n" is, "d" is 9 more than that, or d = n + 9

"twenty-one more quarters than dimes", so, whatever "d" is, "q" is 21 more than that, or q = d + 21

we know, she was just changing the $10, so all nickels and dimes and quarters will add up to 10

thus
`\bf \begin{cases} d=n+9\implies d-9=\boxed{n}\\ \underline{q}=d+21\\\\ d+n+q=10\\ ----------\\ d+\boxed{d-9}+\underline{d+21}=10 \end{cases}`

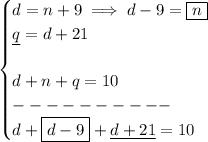
solve for "d", to see how many dimes she gave

what about quarters? well, q = d + 21
and nickels? well, d - 9 = n