Question

You are designing a system for moving aluminum cylinders from the ground to a loading dock. You use a sturdy wooden ramp that is 8.00 m long and inclined at 37.0∘ above the horizontal. Each cylinder is fitted with a light, frictionless yoke through its center, and a light (but strong) rope is attached to the yoke. Each cylinder is uniform and has mass 470 kg and radius 0.300 m. The cylinders are pulled up the ramp by applying a constant force F⃗ to the free end of the rope. F⃗ is parallel to the surface of the ramp and exerts no torque on the cylinder. The coefficient of static friction between the ramp surface and the cylinder is 0.120.

1)What is the largest magnitude F⃗ can have so that the cylinder still rolls without slipping as it moves up the ramp? ____(unit)
2)If the cylinder starts from rest at the bottom of the ramp and rolls without slipping as it moves up the ramp, what is the shortest time it can take the cylinder to reach the top of the ramp? ___(unit)

Answer 1

We are given with
l = 8.00 m
θ = 37.0°
m = 470 kg
r = 0.300 m
μ = 0.120

To solve the magnitude of the force required to roll the cylinders up the ramp, we do a force balance
F = Ff
F = μFn
F = mgμ sin θ
substituting the given values
F = 470 (9.81) (0.120) sin 37.0°
F = 333.97 N

Answer 2

a) F = 321 N , b) t = 0.87 s

Step-by-step explanation:

a) For this exercise we will use Newton's second law, in a reference system with an axis parallel to the ramp (x axis) and the other is perpendicular (y axis)

Y Axisy

N -
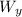`W_(y)` = 0

N =
`W_(y)`

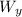
X axis

F - fr- Wₓ = 0

F = fr + Wₓ

The expression for the force of friction is

fr = μ N

Let's use trigonometry to find the weight components

sin37 = Wₓ / W

cos37 =
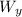`W_(y)` / W

Wₓ = W sin37

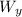`W_(y)` = W cos 37

Let's replace

F = μ W cos 37 + W sin37

F = mg (μ cos37 + sin37)

F = 470 9.8 (0.120 cos 37 + sin37)

F = 321 N

b) For this part we must use the relationship between work and energy

W = ΔEm

The work is

W = F L cos 0 = F L

The initial energy at the bottom is

Em₀ = 0

The energy at the top

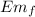`Em_(f)` = K + U = ½ m v² + m g y

Let's look for the height (y) by trigonometry

sin 37 = y / L

y = L sin37

Let's substitute

F L = ½ m v² + m g L sin37 - 0

v² = 2L (F / m - g sin37)

v = √ 2L (F / m - g sin37)

v = √ (2 8 (321/470 - 9.8 sin37) ) = √ ( 16 ( 5.21)

v = 9.13 m / s

As the cylinder rises at a constant speed we can use the ratio

v = d / t

t = d / v

t = L / v

t = 8 / 9.13

t = 0.87 s