Question

What is the equation of the quadratic graph with a focus of (-4,17/8) and a directrix of y=15/8

Answer 1

so hmm notice the graph below

based on where the focus point is at, and the directrix, then, the parabola is opening upwards, meaning the squared variable is the "x"


`\bf \begin{array}{llll} (y-{{ k}})^2=4{{ p}}(x-{{ h}}) \\\\ \boxed{(x-{{ h}})^2=4{{ p}}(y-{{ k}})}\\ \end{array} \qquad \begin{array}{llll} vertex\ ({{ h}},{{ k}})\\\\ {{ p}}=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix} \end{array}`

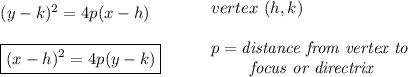
now, keep in mind, the vertex is at coordinates h,k
the vertex itself is half-way between the focus and directrix
the directrix is at y=15/8 and the focus is at y=17/8
so, half-way will then be
`\bf \cfrac{17}{8}-\cfrac{15}{8}=\cfrac{2}{8}\iff \cfrac{1}{4}`

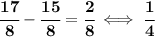
well, so is 1/4 between the focus point and the directrix, half of that is 1/8
so, if you move from the focus point 1/8 down, you'll get the y-coordinate for the vertex, or 1/8 up from the directrix, since the vertex is equidistant to either

what's the "p" distance? well, we just found it, is just 1/8

so, the x-coordinate is obviously -4, get the y-coordinate by 17/8 - 1/8 or 15/8 + 1/8

and plug your values (x-h)² = 4p(y-k) and then solve for "y", that's the equation of the quadratic