Question

A software designer is mapping the streets for a new racing game. All of the streets are depicted as either perpendicular or parallel lines. The equation of the lane passing through A and B is -7x + 3y = -21.5. What is the equation of the central street PQ?

A. -3x + 4y = 3
B.-1.5x − 3.5y = -31.5
C.2x + y = 20
D.-2.25x + y = -9.75

Answer 1

-1.5x − 3.5y = -31.5

Answer 2

Option B is correct .i.e., -1.5x - 3.5y = -31.5

Explanation:

Given: All streets are either parallel or perpendicular.

Equation of Street AB , -7x + 3y = 21.5

To find Equation of Street PQ

Re write the given equation in form of slope and intercept form

we get,

`3y=7x+21.5`

`y=(7)/(3)+(21.5)/(3)`

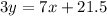
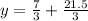
From this slope of street AB is [tex\frac{7}{3}[/tex].

From given pic Street PQ is perpendicular to street AB.

we know that product of slope of perpendicular lines should be equal to -1

let slope of PQ = m

`(7)/(3)* m=-1`

`m=(-3)/(7)`

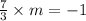
Slope of line in Option A).

`4y=3x+3`

`y=(3)/(4)+(3)/(4)`

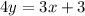
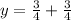
Slope =
`(3)/(4)`

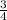
So, this is not required equation.

Slope of line in Option B).

`-3.5y=1.5x-31.5`

`y=(1.5)/(-3.5)+(31.5)/(3.5)`

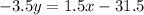
Slope =
`(1.5)/(-3.5)=(3)/(7)`

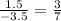
So, this is required equation.

Therefore, Option B is correct .i.e., -1.5x - 3.5y = -31.5