The length of side
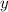 is approximately
is approximately
 when rounded to the nearest tenth.
when rounded to the nearest tenth.
To find the missing side y of the right-angled triangle, we can use the trigonometric functions. Given the angle of
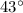 and the opposite side x, we can use the tangent function to find side y. The tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side.
and the opposite side x, we can use the tangent function to find side y. The tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side.
Here's the step-wise method:
1. Set up the equation using the tangent function:
![\[ \tan(43^\circ) = (x)/(y) \]](https://img.qammunity.org/2023/formulas/mathematics/college/jcur19lr90l9koov6lr5opmjkffuzch2qu.png)
2. Since we know the length of the hypotenuse (141), we can use the sine function to find x, and then solve for y using the tangent function. For the sine function:
![\[ \sin(43^\circ) = (x)/(141) \]](https://img.qammunity.org/2023/formulas/mathematics/college/t4651ivpjk88qv6s5tr2wsuchlj9m6esr8.png)
3. Solve for x:
![\[ x = 141 * \sin(43^\circ) \]](https://img.qammunity.org/2023/formulas/mathematics/college/lmviqpnk3xwkhhh6ge0vcqqmh2d3gj4jny.png)
4. Once x is found, rearrange the tangent function to solve for y:
![\[ y = (x)/(\tan(43^\circ)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/pcxp7l38e2adsp5nkx7zn8ll5dunqeb890.png)
5. Plug in the value of x into the equation to find y.
Let's perform the calculations.
To find the missing side y of the right triangle, here are the steps and the calculated values:
1. We set up the equation using the tangent function for angle
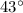 and side x:
and side x:
![\[ \tan(43^\circ) = (x)/(y) \]](https://img.qammunity.org/2023/formulas/mathematics/college/jcur19lr90l9koov6lr5opmjkffuzch2qu.png)
2. We use the sine function to find the length of side x (the side opposite to the
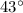 angle):
angle):
![\[ \sin(43^\circ) = (x)/(141) \]](https://img.qammunity.org/2023/formulas/mathematics/college/t4651ivpjk88qv6s5tr2wsuchlj9m6esr8.png)
3. We calculate the length of side x:
![\[ x = 141 * \sin(43^\circ) \]](https://img.qammunity.org/2023/formulas/mathematics/college/lmviqpnk3xwkhhh6ge0vcqqmh2d3gj4jny.png)
![\[ x \approx 96.2 \]](https://img.qammunity.org/2023/formulas/mathematics/college/ibchkk3g1c0wyssj7fodvgee23wwumxqpm.png)
4. We rearrange the tangent function to solve for y:
![\[ y = (x)/(\tan(43^\circ)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/pcxp7l38e2adsp5nkx7zn8ll5dunqeb890.png)
5. We plug in the value of
 into the equation to find y:
into the equation to find y:
![\[ y \approx (96.2)/(\tan(43^\circ)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/illg7dhseqsnxxv65kx4tc9j7ivocmk731.png)
![\[ y \approx 103.1 \]](https://img.qammunity.org/2023/formulas/mathematics/college/htjwuee6hs8p425tspkbrov6niopsq644r.png)
Hence, the answer is approximately
 .
.