Answer with explanation:
We have to prove that
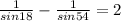
sin54°=sin3×18°=3 sin18°-4sin³18°
LHS
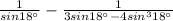
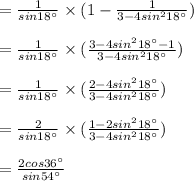
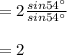
Hence Proved.
Used the following trigonometric Identity to solve the problem
Sin3A=3 SinA-4 sin³A
Sin(90°-A)=Cos A &Cos(90°-A)=SinA
Cos 2A=2Cos²A-1=1-2Sin²A=Cos²A-Sin²A