Question

The axis of symmetry for the graph of the function f(x) = 3x2 + bx + 4 is x = . What is the value of b?

Answer 1

the correct answer is -9

The axis of symmetry for the graph of the function f(x) = 3x2 + bx + 4 is x = . What is the value of b?

⇒ -9

i just took the test

Answer 2

b =-9

Explanation:

Given is an equation of a parabola

`f(x) = 3x^(2) +bx+4`

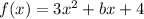
This is a parabola open up

Axis of symmetry is given as x = 3/2

Hence parabola would have equation of the form

`f(x) = a(x-(3)/(2) )^2+k`

`f(x) = ax^2-2ax((3)/(2) )+(9a)/(4) +k`

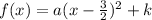
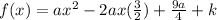
Compare this with the given equation

Equate the coefficient of x square to get

a =3

Equate coefficient of x to get

-3a = b

Or b=-3(3) = -9

Hence value of b =-9