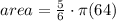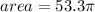1 Answer

Trect · Answer 1 · 2018-11-29T02:00:19+0000

Answer:

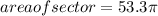
$area of sector=53.3 \pi$

Explanation:

the approximate area of a sector with radius equal to 8 and measure of arc equal to 300°

The radius of a circle is 8

measure of an arc is 300 degree

Now use area of a sector formula

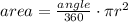
$area=(angle)/(360)  \cdot \pi r^2$

Replace the radius and angle value in the formula

$area=\frac{300{360}  \cdot \pi (8)^2$

$area=(5)/(6)  \cdot \pi (64)$

$area=53.3 \pi$

Please log in or register to add a comment.