Question

Determine the radius and height of the rectangle so as to maximize the area

Answer 1

The perimeter of the shape becomes

`\begin{gathered} P=2h+2r+\text{length of arc } \\ P=2h+2r+(180)/(360)*2*\pi r \\ P=2h+2r+(1)/(2)*2*\pi r \\ P=2h+2r+\pi r \\ 2h+2r+\pi r=920 \\ \text{making h the subject, we have } \\ 2h=920-2r-\pi r \\ \text{dividing both sides by 2} \\ (2h)/(2)=(920)/(2)-(2r)/(2)-(\pi r)/(2) \\ h=460-r-(\pi r)/(2) \end{gathered}`

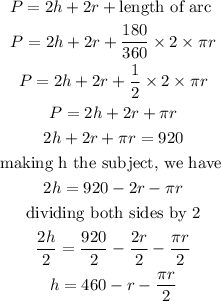
So from the perimeter, we now have an equation to find the height.

Now, let us find the area, A of the figure

`\begin{gathered} A=(2r* h)+(1)/(2)\pi r^2 \\ A=2rh+(1)/(2)\pi r^2 \\ \text{substituting the equation we got for h } \\ A=2r(460-r-(\pi r)/(2))+(\pi r^2)/(2) \\ A=920r-2r^2-\pi r^2+(\pi r^2)/(2) \\ A=920r-2r^2-(\pi r^2)/(2) \\ A=920r-(2+(\pi)/(2))r^2 \end{gathered}`

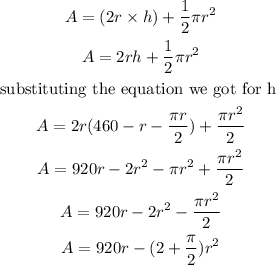
Now, we have the equation for the area

To maximize the area, the derivative of the equation for the area must be equal to zero, so we have

`\begin{gathered} A=920r-(2+(\pi)/(2))r^2 \\ (dA)/(dr)=920-2(2+(\pi)/(2))r=0 \\ 920=2(2+(\pi)/(2))r \\ 460=(2+(\pi)/(2))r \\ r=(460)/((2+(\pi)/(2))) \end{gathered}`

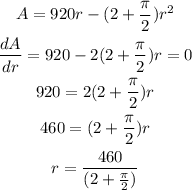
So, from here, we can get r, then substitute the value to get h

Hence from the equation, r becomes

`\begin{gathered} r=(460)/((2+(\pi)/(2))) \\ r=(460)/(3.5707963) \\ r=128.822805 \\ r=128.82\text{ to the nearest hundredth } \end{gathered}`

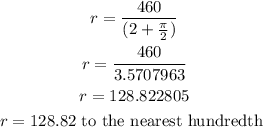
Hence the radius is 128.82 to the nearest hundredth

For the height we have

`\begin{gathered} h=460-r-(\pi r)/(2) \\ h=460-128.822805-(\pi*128.822805)/(2) \\ h=460-128.822805-202.354389 \\ h=128.822806 \end{gathered}`

Hence the height is 128.82 to the nearest hundredth