Answer:
a) E_{z} = 0, b) E_{z} = 0, c) z = 1.73 [1 +
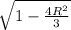 ], d)
], d)
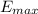 Emax = 9.7 10¹⁰ N / C
Emax = 9.7 10¹⁰ N / C
Step-by-step explanation:
For this exercise we use the expression
E = k ∫ dq / r²
By applying this expression to our problem of a ring of radius R, with a perpendicular axis in the z direction, we can calculate the electric field for a small charge element
dE = k dq / r²
In the attachment we can see a diagram of the electric field, it is observed that the fields perpendicular to the z axis cancel and the field remains in the direction of the axis
d
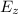 = dE cos φ
= dE cos φ
we substitute
E_{z} = k∫
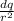 cos φ
cos φ
let's write the expressions
r² = R² + z²
cos φ = z / r
we substitute in the integral, where we see that the load differential does not depend on the distance and the value of the total load is + Q
E_{z} = k
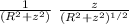 ∫ dq
∫ dq
E_{z} = k Q

This is the expression for the electric field in the axis perpendicular to the ring, we analyze this expression to answer the questions
a) the magnitude of the field at z = 0
E_{z} = 0
b) the magnitude of the field for z = inf
when z »R the expression remains
E_{z} = k
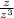 Q
Q
E_{z} = k Q
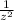
therefore when the value of z = int the field goes to E_{z} = 0
c) In value of z for which the field is maximum.
We have an extreme point when the first derivative is equal to zero
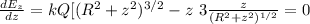
we solve
(R² + z²)^{ 3/2} = 3 z² /(R² +z²) ^{1/2}
(R² + z²)² = 3z²
r² + z² = √3 z
z² –1.732 z + R² = 0
we solve the quadratic equation
z = [1.732 ±
 ]/ 2 = [1.73 ± 1.73
]/ 2 = [1.73 ± 1.73
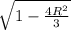 ] / 2
] / 2
z = 0.865 [1 ±
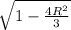 ]
]
Therefore there are two points where the field has an extreme point one, one is a maximum and the other a minimum, as we have already determined a minimum at z = 0 the maximum point must be
z = 0.865 [1 +
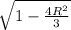 ]
]
d) the value of Emax
z₁ = 0.865 [1+
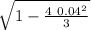 ) = 1.73 [1 + √0.99786]
) = 1.73 [1 + √0.99786]
z₁ = 1.729 m
z₂ = 0.865 [1 - √0.99786 ]
z₂ = 0.0011 m≈ 0
for which the field has a maximum value substituting in equation 1
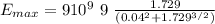
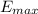 = 81 10⁹
= 81 10⁹

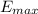 Emax = 9.7 10¹⁰ N / C
Emax = 9.7 10¹⁰ N / C