Question

An author receives $0.60 for each hardcover book or paperback book that is sold. there were x hardcover books and 38,000 paperback books sold of her most recent book. the author received a total of $51,000 for the book sales. the equation below can be used to determine the number of hardcover books that were sold. 0.60(x 38,000) = 51,000 how many hardcover books were sold?

Answer 1

Since an author receives $0.60 for either hardcover or paperback book sold, we can develop an equation: 0.60(x + 38 000) = 51 000
x + 38 000 = 85 000
x = 85 000 - 38 000 = 47 000

Hence, there were 47 000 hardcover books sold.

Answer 2

47,000 books.

Explanation:

The given equation is

`0.60(x + 38 000) = 51 000`

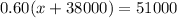
Where
`x` represents the number of hardcover books sold. To find the answer we just have to isolate the variable and solve.

First, we apply distributive property

`0.60x+22800=51000`

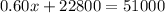
Now, we isolate
`x`

`0.60x=51000-22800\\0.60x=28200\\x=(28200)/(0.60)=47000`

This result means that the author sold 47000 hardcover books, which make him to gain $51000.

Therefore, the answer is 47,000 books.