Question

Write in simplest form:

`\sqrt[3]{24a^(10)b^(6)}`

Please explain :D

Answer 1

`2a^3b^2\sqrt[3]{3a}`

Explanation:

Use the following rules for exponents:

`a^m*a^n=a^(m+n)\\\\\sqrt[3]{x^3}=x`

Simplify 24. Find two factors of 24, one of which should be a perfect cube:

`8*3=24\\\\2^3=8`

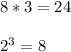
Insert:

`\sqrt[3]{2^3*3a^(10)b^6}`

Now split the exponents. Split 10 into as many 3's as possible:

`10=3+3+3+1`

Insert as exponents:

`\sqrt[3]{2^3*3*a^3*a^3*a^3*a^1*b^6}`

Split 6 into as many 3's as possible:

`6=3+3`

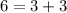
Insert as exponents:

`\sqrt[3]{2^3*3*a^3*a^3*a^3*a^1*b^3*b^3}`

Now simplify. Any terms with an exponent of 3 will be moved out of the radical (rule #2):

`2\sqrt[3]{3*a^3*a^3*a^3*a^1*b^3*b^3}\\\\\\2*a*a*a\sqrt[3]{3*a^1*b^3*b^3}\\\\\\2*a*a*a*b*b\sqrt[3]{3*a^1}`

Simplify:

`2a^3b^2\sqrt[3]{3a}`

:Done