Question

Write a polynomial function of least degree with integral coefficients that has the given zeros 2,-1,-5

Answer 1

Since it has zeros at x = 2, -1, and -5, then by definition, (x - 2), (x + 1), and (x + 5) are factors of the polynomial.

A standard polynomial is in the form:


`P(x) = Q(x)D(x) + R(x)`
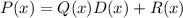
Since R(x) = 0, then


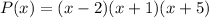
`P(x) = (x - 2)(x + 1)(x + 5)` and you can just expand that out to get a cubic polynomial, as expected.

Answer 2

We have the zeroes of this function:
x 1 = 2, x 2 = - 1, x 3 = - 5
Polynomial of least degree is in form:
p ( x ) = a x³ + b x² + c x + d
Three factors of the polynomial are:
( x - x1 ) * ( x - x2 ) * ( x - x3 ) =
= ( x - 2 ) · ( x + 1 ) · ( x + 5 ) =
= ( x² + x - 2 x - 2 ) · ( x + 5 ) =
= ( x² - x - 2 ) · ( x + 5 ) =
= x³ + 5 x² - x² - 5 x - 2 x - 10 = x³ + 4 x² - 7 x - 10
Answer: The polynomial of least degree with integer coefficients is:
p ( x ) = x³ + 4 x² - 7 x - 10.