Question

Which of the following results in the difference of two squares? -the options are in the picture

Answer 1

Special Products

Some products of polynomials are so common that we learn them by heart for easy use.

The following are some cases of special products:

`\begin{gathered} (a+b)(a-b)=a^2-b^2 \\ (a+b)^2=a^2+2ab+b^2 \\ (a-b)^2=a^2-2ab+b^2 \end{gathered}`

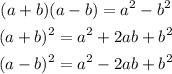
From the list above, only one of them, the first one, results in the difference of two squares.

Paying close attention to the structure of the product, we find its two factors are almost identical, except for the sign that connects the terms in parentheses.

We only have to find the option that has a product of two binomials, one with its terms being added, and the other with its terms being subtracted.

The only option that satisfies the condition is:

`(3x+7y)(3x-7y)`

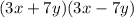
That results in:

`(3x+7y)(3x-7y)=9x^2-49y^2`

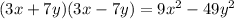
The difference of two squares, as required