Question

Find a power series representation for the function and determine the interval of convergence ln(5 - x

Answer 1

To find the power series representation of In(5 - x), we recall that the power series representation of a function of the form:

`(a)/(1-r) =\sum\limits^\infty_(n=0)ar^n`
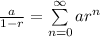
provided |r| < 1
Also recall that

`\int{(a)/(1-r)\,dx} =\int{\sum\limits^\infty_(n=0)ar^n\,dx}`
Notice that

`ln((5-x))=-\int {(1)/(5-x)\,dx}`
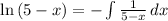
To get the power series of

`(1)/(5-x)= ((1)/(5)) (1)/(1- (x)/(5) ) \\ =\sum\limits^\infty_(n=0)( (1)/(5)) ((x)/(5))^n=((1)/(5)) ((x)/(5))+((1)/(5)) ((x^2)/(25))+((1)/(5)) ((x^3)/(125))+ . . . \\ =(x)/(25)+(x^2)/(125)+ (x^3)/(625)+ . . .`
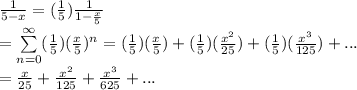
Therefore, the power series representation of

`ln((5-x))=-\int {(1)/(5-x)\,dx} \\ =-\int{((x)/(25)+(x^2)/(125)+ (x^3)/(625)+ . . . ),dx} \\ =C-(x^2)/(50)-(x^3)/(375)- (x^4)/(2500)- . . .`
When x = 0: C = ln 5
Therefore,

`ln((5-x))=ln(5)-(x^2)/(50)-(x^3)/(375)- (x^4)/(2500)- . . .`

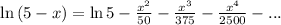
The radius of convergence is given by |r| < 1.
Here,

`r= (x)/(5)`
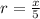
Therefore, radius of convergence is

`| (x)/(5)| \ \textless \ 1 \\ |x|\ \textless \ 5`