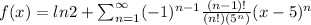Question

Find the taylor series for f(x centered at the given value of

a. [assume that f has a power series expansion. do not show that rn(x ? 0. ] f(x = ln x, a = 5

Answer 1

To find the Taylor series for f(x) = ln(x) centering at 5, we need to observe the pattern for the first four derivatives of f(x). From there, we can create a general equation for f(n). Starting with f(x), we have


`f(x) = ln(x) \\ f^(1)(x) = (1)/(x) \\ f^(2)(x) = -(1)/(x^(2)) \\ f^(3)(x) = (2)/(x^(3)) \\ f^(4)(x) = (-6)/(x^(4))`
.
.
.
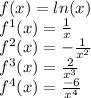
Since we need to have it centered at 5, we must take the value of f(5), and so on.


`f(5) = ln(5) \\ f^(1)(5) = (1)/(5) \\ f^(2)(5) = (-1)/(5^(2)) \\ f^(3)(5) = (1(2))/(5^(3)) \\ f^(4)(5) = (-1(2)(3))/(5^(4))`
.
.
.
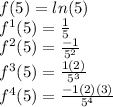
Following the pattern, we can see that for
`f^(n)(x)`,


`f^(n)(x) = (-1)^(n-1) (1(2)(3)...(n-1))/(5^(n)) \\ f^(n)(x) = (-1)^(n-1) ((n-1)!)/(5^(n))`

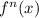
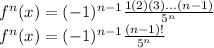
This applies for
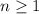
`n\geq 1`. Expressing f(x) in summation, we have


`\sum_(n=0)^(\infty) (f^(n)(5))/(n!) (x-5)^(n)`

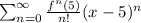
Combining ln2 with the rest of series, we have


`f(x) = ln2 + \sum_(n=1)^(\infty) (-1)^(n-1) ((n-1)!)/((n!)(5^(n))) (x-5)^(n)`

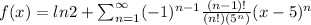
Answer:
`f(x) = ln2 + \sum_(n=1)^(\infty) (-1)^(n-1) ((n-1)!)/((n!)(5^(n))) (x-5)^(n)`