We can calculate the energy of a single photon through Plank-Einstein relation. We have

where
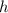
is the Plank's constant and

is the frequency. Also, recall that to solve for the frequency, we have
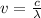
where

is the speed of light and
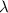
is the wavelength of the laser, in meters. So for this problem we can compute for

with

Going back to the Planck-Einstein relation, we have
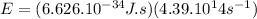
Hence, we have
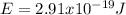
.
Given that the laser emits an energy of 0.258 J, then there are
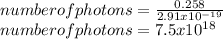
.
Answer: 7.5 ⋅ 10^18 photons