Question

How to find the asymptotes of a hyperbola?

Answer 1

To find the asymptotes of a hyperbola, you need to consider the equation of the hyperbola. The asymptotes are the lines that the hyperbola approaches as the x and y values become very large or very small.

Step-by-step explanation:

To find the asymptotes of a hyperbola, you need to consider the equation of the hyperbola. The general equation of a hyperbola is given by (x-h)²/a² - (y-k)²/b² = 1 or (y-k)²/a² - (x-h)²/b² = 1, where (h,k) is the center of the hyperbola, a is the distance from the center to the vertices in the x-direction, and b is the distance from the center to the vertices in the y-direction.

The asymptotes of a hyperbola are the lines that the hyperbola approaches as the x and y values of the hyperbola become very large or very small. The equations of the asymptotes are given by y = k ± (b/a)(x-h).

For example, let's consider the hyperbola given by (x-2)²/9 - (y+1)²/4 = 1. The center of the hyperbola is (2,-1), a = 3, and b = 2. The equations of the asymptotes would be y = -1 ± (2/3)(x-2).

Answer 2

Vertical asymptote:
Find the restriction on x. This is the easiest of the three asymptotes you will need to find (even if only two can show at a time). As a hyperbola is in the form:
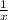
`(1)/(x)`, you only need to find the restriction on the denominator, namely denominator can never be zero. Hence, let the denominator equal to zero to find the vertical asymptote.

Horizontal asymptote:
Find the restriction on y. To do this, you need to simplify the top and bottom to its lowest terms. If it simplifies to a form such as:
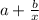
`a + (b)/(x)`, then the horizontal asymptote becomes y = a. You need to think to yourself, as x grows to infinite, and shrinks to negative infinite, what happens to the function? Does it slowly curve to a stop?

Oblique asymptote:
This is a pretty rare kind, but it still exists, so don't be naive to this sort of asymptote. This is a form of horizontal and vertical asymptote, only it's at an angle. That is, this asymptote is a set of x and y-coordinates that work in unison to produce a curvature or line.

Let's consider:
`f(x) = (x^(2) - 6x + 7)/(x + 5)`

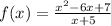
Now, in normal term, a horizontal asymptote would have a degree higher in the denominator than in the numerator. However, it's flipped in this case.

Now, you will need to long divide this set of polynomials to yield a straight y = x line, except it's been moved 11 units to the right to yield a y = x - 11 line.

Remember: these exist because the highest power is in the numerator and not the denominator.