Question

Find all the missing elements:B.aC = 120°b = 5C = 11Аb CA = [?]° B = [ ]º a =a = [ ]Round to the nearest tenth.

Answer 1

To solve, this problem we will use the sine rule:

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

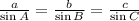
First, let us solve for B, We will relate:

`\begin{gathered} (b)/(\sin B)=(c)/(\sin C) \\ since\text{ the c part of the formula is complete} \end{gathered}`
`\begin{gathered} (5)/(\sin B)=(11)/(\sin 120) \\ \text{Cross multiply} \\ 5*\sin 120=11*\sin B \\ \end{gathered}`
`\begin{gathered} 4.33013=11\sin B \\ (4.33013)/(11)=\sin B \\ 0.393648=\sin B \\ \sin ^(-1)(0.393648)=B \\ 23.1817^o=B \\ 23.2^o(to\text{ the nearest tenth)=B} \end{gathered}`

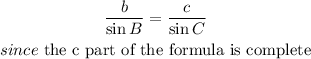
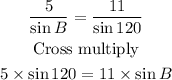
B = 23.2 degrees.

To find A, we will use the sum of angles in a triangle:

`A+B+C=180^o`
`\begin{gathered} A+23.2+120=180 \\ A=180-120-23.2 \\ A=36.8^o \end{gathered}`

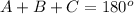
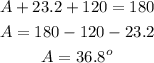
A = 36.8 degrees.

To find a, we will use the sin rule again.

`\begin{gathered} (a)/(\sin A)=(c)/(\sin C) \\ (a)/(\sin36.8)=(11)/(\sin 120) \end{gathered}`

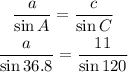
Cross multiply:

`\begin{gathered} a*\sin 120=11*\sin 36.8 \\ a=(11*\sin 36.8)/(\sin 120) \\ a=(11*0.599024)/(0.866025) \\ a=(6.589264)/(0.866025) \end{gathered}`
`\begin{gathered} a=7.6086 \\ a=7.6(to\text{ the nearest tenth)} \end{gathered}`

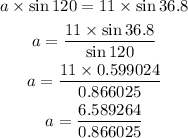
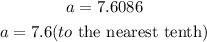
a=7.6

Final answers:

A=36.8 degrees, B=23.2 degrees, a=7.6