Question

A given curve in the family x^2 + xy + ay^2 = b has a tangent line at point (1,3) with slope -5/14. What are the values of a and b?

Answer 1

assuming a and b are constants

take derivitive

2x+y+x(dy/dx)+2ay(dy/dx)=0
2x+y=-x(dy/dx)-2ay(dy/dx)

`(2x+y)/(-x-2ay)= (dy)/(dx)`

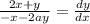
at (1,3) the slope is -5/14



`(2(1)+(3))/(-1-2a(3))= (-5)/(14)`

`(2+3)/(-1-6a)= (-5)/(14)`

`(5)/(-1-6a)= (-5)/(14)`

`(-5)/(1+6a)= (-5)/(14)`
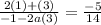
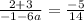
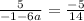
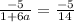
1+6a=14
6a=13
a=13/6

sub back

x^2+xy+(13/6)y^2=b
a point is (1,3)
1+(1)(3)+(13/6)(3)^2=b
1+3+39/2=b
8/2+39/2=b
47/2=b


a=13/6
b=47/2