Question

2. f is a differentiable function on the interval [0, 1] and g(x) = f(3x). The table below gives values of f '(x). What is the value of g '(0.1)? (4 points)

x 0.1 0.2 0.3 0.4 0.5
f '(x) 1 2 3 -4 5

A 1
B 3
C 9
D Cannot be determined

Answer 1

Chain rule:


`g(x)=f(3x)\implies g'(x)=3f'(3x)`

so


`g'(0.1)=3f'(0.3)=3(3)=9`

Answer 2

Option C.

Explanation:

It is given that f is a differential function on the interval [0, 1].

`g(x)=f(3x)`

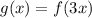
Differentiate with respect to x.

`g'(x)=f'(3x)(d)/(dx)(3x)`

`g'(x)=3f'(3x)`

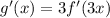
We need to find the value of f'(0.1).

Substitute x=0.1 in the above equation.

`g'(0.1)=3f'(3(0.1))`

`g'(0.1)=3f'(0.3)`

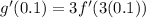
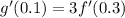
From the given table it is clear that f'(0.3)=3.

`g'(0.1)=3(3)`

`g'(0.1)=9`

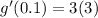
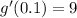
The value of g'(0.1) is 9.

Therefore, the correct option is C.