Question

Write the function or evaluate for each of the below

Answer 1

`\begin{gathered} (e)2x^3-10x^2 \\ \text{ }(f)(2x^2)/(x-5),x\\eq5\; \; \; \mleft(g\mright)5\text{ } \\ (h)(f\circ g)(x)=2x^2-5 \\ (I).(g\circ f)(x)=2x^2-20x+50 \\ (J).\text{ }(f\circ g)(3)=13 \end{gathered}`

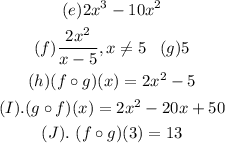
Explanation:

Given the functions f(x) and g(x) below:

`\begin{gathered} f(x)=x-5 \\ g(x)=2x^2 \end{gathered}`

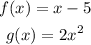
Part E (f * g(x)

`\begin{gathered} (f\cdot g)(x)=f(x)\cdot g(x) \\ =\lbrack x-5\rbrack\lbrack2x^2\rbrack \\ =2x^3-10x^2 \end{gathered}`

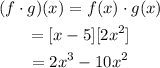
Part F (g ÷ f)(x)

`\begin{gathered} (g/ f)(x)=(g(x))/(f(x)) \\ =(2x^2)/(x-5) \end{gathered}`

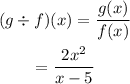
Part G

When the denominator of a rational function is 0, the function is Undefined.

The denominator of (g ÷ f)(x) = x-5

`\begin{gathered} x-5=0 \\ \implies x=5 \end{gathered}`

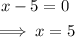
The value of x that cannot be inputed into (g ÷ f)(x) is 5.

Part H (f o g)(x)

`\begin{gathered} (f\circ g)(x)=f\lbrack g(x)\rbrack \\ f(x)=x-5 \\ \implies f\lbrack g(x)\rbrack=g(x)_{}-5=2x^2-5 \\ Therefore\colon \\ (f\circ g)(x)=2x^2-5 \end{gathered}`

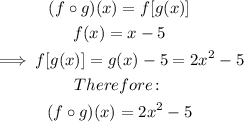
Part I (g o f)(x)

`\begin{gathered} (g\circ f)(x)=g\lbrack f(x)\rbrack \\ g(x)_{}=2x^2 \\ \implies g\lbrack f(x)\rbrack=2\lbrack f(x)\rbrack^2_{}=2(x-5)^2 \\ =2\mleft(x-5\mright)\mleft(x-5\mright) \\ =2\mleft(x^2-10x+25\mright) \\ Therefore\colon \\ (g\circ f)(x)=2x^2-20x+50 \end{gathered}`

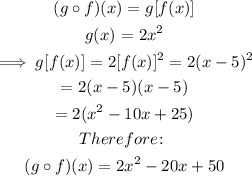
Part J

From part H:

`(f\circ g)(x)=2x^2-5`

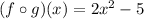
Substitute 3 for x to get (f o g)(3).

`\begin{gathered} (f\circ g)(3)=2(3)^2-5 \\ =2(9)^{}-5 \\ =18-5 \\ (f\circ g)(3)=13 \end{gathered}`

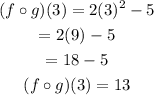
The value of (f o g)(3) is 13.