Question

Which of the following describes the roots of the polynomial function f(x) = (x-3)^4(x+6)^2

Answer 1

write out every grouping

(x-3)(x-3)(x-3)(x-3)*(x+6)(x+6)

and multiply

4x^2+3x+63

Answer 2

3,3,3,3 ,-6, and -6.

Explanation:

Given the polynomial function

f(x) =
`(x-3)^4(x+6)^2`

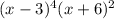
To find the roots of given polynomial we put f(x)=0

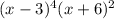`(x-3)^4(x+6)^2`=0

Then we put

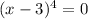`(x-3)^4=0` and
`(x+6)^2=0`

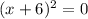
Now, we put each factor of (x-3 )equal to zero

x-3=0

x=3

x-3=0

x=3

x-3=0

x=3

x-3=0

x=3

Similarly , we put each factor of (x+6 ) equal to zero

Then we get

x+6=0

x=-6

x+6=0

x=-6

Multiplycity of 3=4

Multiplicity of -6= 2.

Multiplicity of any number is defined as the number of repeatation of that number in polynomial function.

Therefore, the roots of given polynomial function are 3,3,3,3-6 and -6.