Question

A researcher measures 200 counts per minute coming from a radioactive source at noon. At 3:00pm, she finds that this has dropped to 25 counts per minute. What percentage of the original source will remain at 6:00pm?

Answer 1

1.5% will remain at 6.00pm.

Explanation:

The function for exponential decay is,

`y(t)=Ae^(rt)`

where,

y(t) = the future amount,

A = initial amount,

r = rate of growth,

t = time.

A researcher measures 200 counts per minute coming from a radioactive source at noon.

At 3:00pm, i.e after 3 hours,she finds that this has dropped to 25 counts per minute.

Putting the values,

`\Rightarrow 25=200e^(r* 3)`

`\Rightarrow \ln (25)/(200)=\ln e^(r* 3)`

`\Rightarrow \ln (1)/(8)={r* 3}* \ln e`

`\Rightarrow \ln (1)/(8)={r* 3}* 1`

`\Rightarrow \ln (1)/(8)={r* 3}`

`\Rightarrow r=(\ln (1)/(8))/(3)=-0.6931`

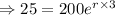
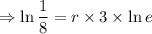
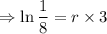
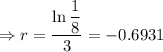
-ve sign means the amount is decreasing.

As we have to find the amount at 6.00pm i.e after 6 hours, so

`y(t)=200e^(-0.6931* 6)=3.13\approx 3`

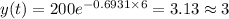
As number of bacteria can't be in decimal.

So the percentage will be,

`=(3)/(200)=0.015=1.5\%`

Answer 2

1.56% 1/8 of the original source (25 counts) remains at 3:00pm. This means that the half-life is 1 hour. Continue to find the fraction at 6:00pm.