Answer:
Part 1)
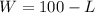
Part 2)

Step-by-step
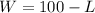 explanation:
explanation:
We are given a rectangle with a perimeter of 200 feet.
Part 1)
The formula for perimeter for a rectangle is:
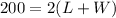
We can divide both sides by 2:
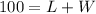
And subtracting L from both sides yields:
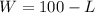
Part 2)
The area of a rectangle is given by:
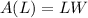
Since we solved for W earlier:
