Question

The table below represents the closing prices of stock ABC for the last 5 days. What is the r-value of the linear regression that fits these data:

Day Value
1 472.08
2 454.26
3 444.95
4 439.49
5 436.55

Answer 1

The r-value of the linear regression that fits these data is -0.947110707.

Explanation:

The linear regression equation is in the form of

`y=bx+a`

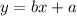
Where,

`b=(n(\sum xy)-(\sum x)(\sum y))/(n(\sum x^2)-(\sum x)^2)`

`a=((\sum y)(\sum x^2)-(\sum x)(\sum xy))/(n(\sum x^2)-(\sum x)^2)`

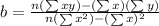
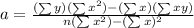
The formula of r is

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n(\sum x^2)-(\sum x)^2][n(\sum y^2)-(\sum y)^2]))`

The values are

`\sum x=15,\sum y=2247.35,\sum x^2=55,\sum y^2=1010938.423,\sum xy=6656.18, n=5`

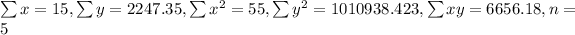
Using above formula, we get

`r=-0.947110707`

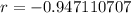
Therefore the r-value of the linear regression that fits these data is -0.947110707.

Answer 2

To answer this one, you may use scientific calculator that is capable of generating the value of r in the regression. We let the day be the values of x and the value be the values of y. By performing the task in the scientific calculator, it was found out that the value of r is -0.947.