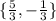Answer:
Option A is correct.
Explanation:
Given the equation:
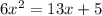
we can write this as:
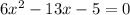
A quadratic equation is of the form:
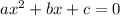
then the solution is given by:
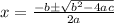
On comparing with the given equation we have;
a = 6, b = -13 and c = -5 then;
Substitute the given values we have
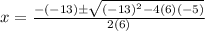
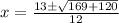
Simplify:
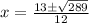
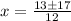
Then;
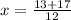 and
and
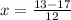
⇒
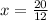 and
and
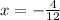
⇒
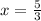 and
and
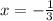
Therefore, the solution for the given equation are: