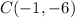Question

Square RSTU is translated to form R'S'T'U', which has vertices R'(–8, 1), S'(–4, 1), T'(–4, –3), and U'(–8, –3). If point S has coordinates of (3, –5), which point lies on a side of the pre-image, square RSTU?

A.(–5, –3)
B.(3, –3)
C.(–1, –6)
D.(4, –9)???????????????

Answer 1

Step 1

Find the rule of the translation of the pre-image to the image

we know that

the point S has coordinates of (
`(3,-5)`

the point S' has coordinates of (
`(-4,1)`

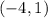
so

a) the rule of the translation of the pre-image to the image is

`(x,y)------> (x-7,y+6)`

Step 2

Find the rule of the translation of the image to the pre-image

a) the inverse rule of the translation of the image to the pre-image is

`(x',y')------> (x'+7,y'-6)`

Step 3

Find the coordinates of the vertices of the pre-image

Applying the inverse rule of the translation of the image to the pre-image

a) Point
`R'(-8,1)`

`R(-8+7,1-6)=R(-1,-5)`

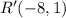
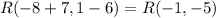
b) Point
`T'(-4,-3)`

`T(-4+7,-3-6)=T(3,-9)`

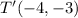
c) Point
`U'(-8,-3)`

`U(-8+7,-3-6)=U(-1,-9)`

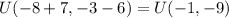
Step 4

Using a graphing tool

graph the points of the pre-image and the points A,B,C and D to determine the solution of the problem

we have

`R(-1,-5) \\S(3,-5)\\T(3,-9)\\U(-1,-9)\\ \\A(-5,-3)\\B(3,-3)\\C(-1,-6)\\D(4,-9)`

see the attached figure

therefore

the answer is the option

`C(-1,-6)`