Answer: The correct option is (B) 55.
Step-by-step explanation: We are given two similar triangles ABC and DEF.
We are to find the value of x.
From the figure, we note that
DE = 6 units, DF = 11 units, AB = 30 units and AC = x units.
We know that the corresponding sides of two similar triangles are proportional.
So, from ΔDEF and ΔABC, we get
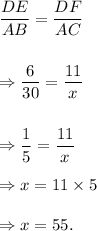
Thus, the value of x is 55 units.
Option (B) is CORRECT.