Question

True or False? The number 1 is an upper bound for the set of roots of this polynomial function. f(x)=3x^4-5x^3-5x^2+5x+2

Answer 1

The answer is false.

Answer 2

False

Explanation:

We are given that the number 1 is an upper bound for the set of roots of this polynomial function

`f(x)=3x^4-5x^3-5x^2+5x+2`

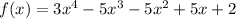
We have to find the statement is false or true.

Substitute x=1 then we get

`f(x)=3(1)-5(1)-5(1)+5(1)+2`

`f(x)=3-5-5+5+2=0`

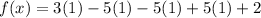
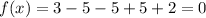
Hence, 1 is the root of the given polynomial

Now substitute x=2 then we get

`f(x)=3(2)^4-5(2)^3-5(2)^2+5(2)+2`

`f(x)=48-40-20+10+2=60-60=0`

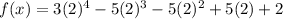
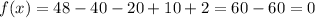
Hence, 2 is also root of the given polynomial .

Upper bound: It is defined as the highest value of the set and all values in the set are less than the upper bound .

Here we have find two roots but 2 is greater than 1 . So 1 is not the upper bound for the set of roots of polynomial .

Hence, it is false.

Answer : False