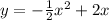Question

A parabola has its vertex at (2, 2), and the equation of its directrix is y = 2.5. The equation that represents the parabola is

Answer 1

In vertex form the equation is
`y=-(1)/(2)(x-2)^2+2`

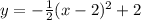
In standard form the equation is
`y=-(1)/(2)x^2+2x`

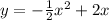
Explanation:

The equation of the directrix tells us that this is an x-squared parabola. Because the directrix is above the vertex, the parabola will open downward. The vertex form of this equation is:

`4p(y-k)=-(x-h)^2`

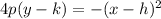
where p is the number of units between the directrix and the vertex. The number of units here is .5 or 1/2. Filling in the coordinates of the vertex and the p value of 1/2:

`4(.5)(y-2)=-(x-2)^2`

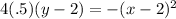
Simplifying we have:

`2(y-2)=-(x-2)^2`

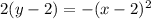
Divide both sides by 2 to get:

`y-2=-(1)/(2)(x-2)^2`

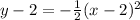
Add 2 to both sides to get the final vertex form:

`y=-(1)/(2)(x-2)^2+2`

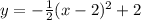
If you want that in standard form, you first need to expand the squared term to get:

`y=-(1)/(2)(x^2-4x+4)+2`

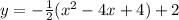
Order of operations tells us that we have to distribute in the -1/2 first to get:

`y=-(1)/(2)x^2+2x+2-2`

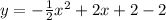
which simplifies to the standard form:

`y=-(1)/(2)x^2+2x`